ちょっと思い出してきたので今回は原始ピタゴラス数の探索について書こうと思います。
高校生の頃に原始ピタゴラス数の探索をしていたことがありました。ピタゴラス数というのは a2+b2=c2 を満たす自然数の組で、各辺の長さの比がこれになっている三角形は直角三角形になります。(3, 4, 5)などのいくつかは学校でも習いますね。
ある時もっとあるだろうから探してみようと思い立ちました。
当然パソコンを使って探すわけですが、当時手元にあって使えたのはPC-8001mk2かFP-1100くらい(FM-7はまだなかったと思う)でした。ある理由(後述)でFP-1100の方が良いのですが、遅かったことやFDDが無かったことなどでPC-8001mk2を使いました。言語も当時使えたのはBASICのみ(平方根を使いたいのでTL/1, GAMEは不向き)でした。
最初に書いたのはおそらく a と b を2重FORループで回しながら c を求めてそれが整数になっているか調べるものだったと思います。
これは簡単なようですが意外と奥が深いです。C=SQR(A^2+B^2)で求めて、IF C=INT(C) THEN ~で判定しようとしてもうまく行きません。
当時は浮動小数点数の扱いについてよくわかっておらず、いろいろな落とし穴に落ちて難しさを実感した思い出です。
まずA^2が危ない、内部的にはAを2回かけるわけではなく指数関数の底の変換を使って求めているはずです。実際2^13を求めるとこんな結果になります。
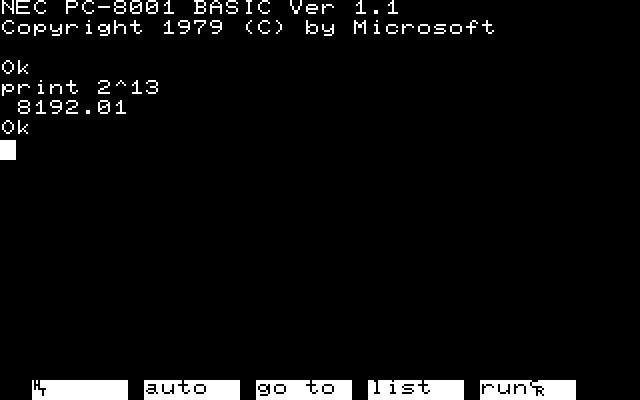
A^2はA*Aに書き換えます。整数処理にできるので速度的にも有利と思います。
続いて整数かどうかの判定ですが簡単なテストプログラムを書いてみました。
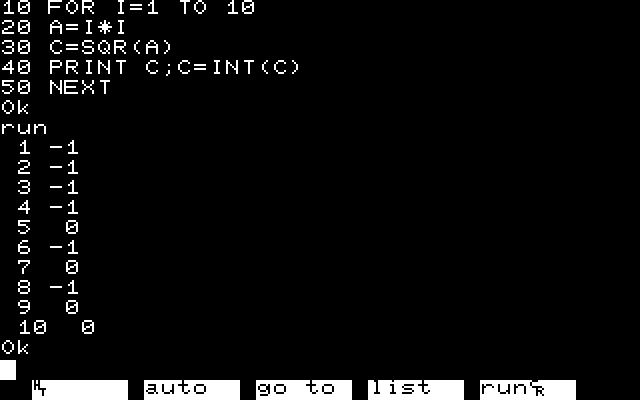
Aは平方数で、Cはその平方根です。当然Cは整数になるはずで、確かに整数として表示されますが、内部表現としては少し異なるようで整数化して比較すると一致しません。(BASICの比較演算では真が-1, 偽が0になります)もちろん差が一定値以下なら一致とみなすようなことをすればいいのですが、当時そこまで考えが及ばず整数化してから再度(上記に注意して)二乗して元に戻るかで判定しました。
これらの点で10進演算のFP-1100なら悩まなくて済んだのかもしれませんが......
これで一通り計算できるようになりましたが、これだとcが180程度で符号付16ビットの整数型の上限を超えてしまいます。後述するように当時の探索結果の一部が残っているのですが(1729, 30480, 30529)などというのが含まれており何らかの工夫をしていたようです。
うっすらと覚えているのは a2 + (2ax+x2) = (a+x)2 を利用して 2ax+x2 が平方数なら(a, √(2ax+x2), (a+x)) がピタゴラス数になるというのを利用したような......
計算とは関係ない工夫もしてありました。
実行中に「カナキー」をロック(PC-8001mk2のカナキーはメカニカルロックです)しておくとキリのいいところで停止し、次に実行すると続きから計算するようにしていました。
当時これを実行していたPC-8001mk2は私のメインマシンでして、またこれ非常に時間のかかるプログラム(一か月以上かかったような記憶)なので、その間使えないのはさすがに困ります。なので使いたいときは止めて、寝ている間や学校に行っている間に計算させていました。
さらに高速化のために6MHzにクロックアップした上にDMA停止していました。
さて、手元にないと書いた当時のコードですが、当時のフロッピー(ほぼ捨てていないはず)のどこかにはあると思うのですが以前一部をイメージ化したファイルには見当たりませんでした。有望なのは漢字ROM すべて発見のところでラベル写真を載せた8インチフロッピーの中ですが、今からこれを読むのはハードル高いですね。計算結果も入っているのではと思います。
NEC NK3618-21 マニュアルに載せた連続紙の写真、あれが計算結果をプリントした紙でして、一部しか撮影していませんが捨ててはいないのでまた出てきたら全ページ撮っておこうと思っています。
コメントを追加